고정 헤더 영역
상세 컨텐츠
본문
https://www.acmicpc.net/problem/2133
2133번: 타일 채우기
문제 3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자. 입력 첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다. 출력 첫째 줄에 경우의 수를 출력한다. 예제 입력 1 복사 2 예제 출력 1 복��
www.acmicpc.net
개어렵다.......... 도저히 못하겠어서 유튜브에 검색해서 강의를 봤다.(https://www.youtube.com/watch?v=RwhY6Ni6iEY) 도움이 많이 되는 영상이다. 2*n 타일링과의 가장 주된 차이점은 예외가 존재한다는 것이다. 이 때문에 굉장히 어려웠다.
#include <iostream>
using namespace std;
const int MAX = 30 + 1;
int N;
int cache[MAX];
void tiling()
{
cache[0] = 1; //cache[1]이 0인 상태에서 cache[0] 마저 0이된다면 계속 2배를 해봐야 0을 2배하는 꼴만 된다.
cache[2] = 3;
for (int i = 4; i <= N; i += 2)
{
cache[i] = cache[i - 2] * cache[2];
for (int j = 0; j <= i - 4; j += 2)
{
cache[i] += cache[j] * 2;
}
}
cout << cache[N];
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cin >> N;
tiling();
}
- n=2일때

이런 모양 3개가 된다.
- n=4일때
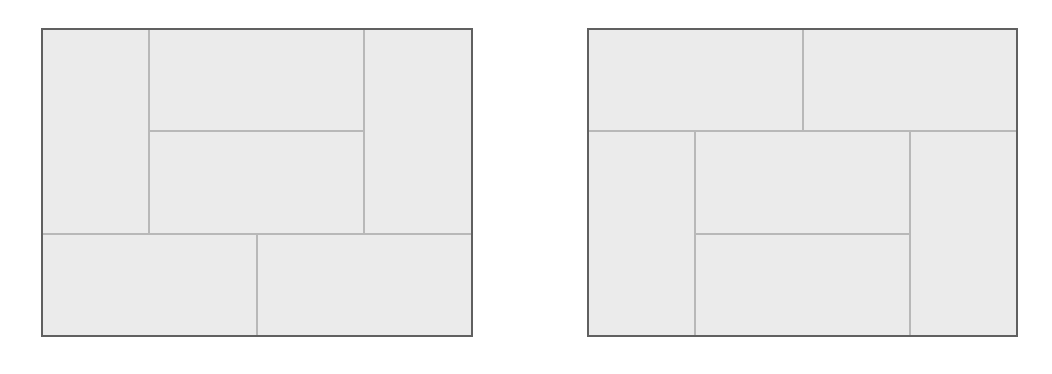
n=4일 때는 n=2일 때 나올 수 있는 경우를 두번 사용하므로 경우의 수는 3*3=9 거기에 이 예외 두 개를 해서 총 11개의 경우가 나온다.
즉, dp[i] = dp[i-2] * 3 (dp[i]는 dp[i-2]에서 두 칸이 늘어나는 것이고 두 칸이 늘어날 경우 경우의 수는 dp[2]인 3이 될 것이다.)
여기에 예외로 생기는 2개씩을 계산해주어야 한다. 2칸일 때는 예외가 존재하지 않기 때문에 최소 4칸은 확보가 되었을 때만 예외 계산을 해준다. 4칸 이상부터 계속해서 예외는 2개씩 발생하고 경우의 수를 2배씩 증가시킨다.
j=0부터 시작하는 이유는 자기 자신의 예외 2개가 더해지게 만들기 위해서이다.
//이 문제는 그림을 그렸을 때 잘 풀린다(아래와 같은 형태로 풀면 쉽게 풀린다)
//■■는 1*2, ㅁ는 2*1 직사각형
// ㅁ
/*
3*2의 경우 = 3가지
■■ ㅁㅁ ■■
ㅁㅁ ㅁㅁ ■■
ㅁㅁ ■■ ■■
*/
/*
3*4의 경우 = 11가지
(3*2의 경우)*(3*2의 경우) = 9가지
+
3*4의 고유 모양 = 2가지
■■■■ ㅁ■■ㅁ
ㅁ■■ㅁ ㅁ■■ㅁ
ㅁ■■ㅁ ■■■■
*/
/*
3*6의 경우 = 41가지
(3*2의 경우)*(3*4의 경우) = 33가지
+
(3*4의 고유 모양)*(3*2의 경우) = 6가지
+
3*6의 고유 모양 = 2가지
■■■■■■ ㅁ■■■■ㅁ
ㅁ■■■■ㅁ ㅁ■■■■ㅁ
ㅁ■■■■ㅁ ■■■■■■
*/
/*
3*8의 경우 = 153가지
(3*2의 경우)*(3*6의 경우) = 123가지
+
(3*4의 고유 모양)*(3*4의 경우) = 22가지
+
(3*6의 고유 모양)*(3*2의 경우) = 6가지
+
3*8의 고유 모양= 2가지
■■■■■■■■ ㅁ■■■■■■ㅁ
ㅁ■■■■■■ㅁ ㅁ■■■■■■ㅁ
ㅁ■■■■■■ㅁ ■■■■■■■■
*/
출처: https://jaimemin.tistory.com/330 [꾸준함]
자주 참고하는 블로그에 있는 설명이다. 이 설명이 이해하는데 굉장히 도움이 되었다. 이 설명에서 고유 모양이라고 하는 것들은 모두 2를 의미한다.
솔직히 이 문제 너무 어렵다. 자주 보면서 고민해봐야겠다.
'알고리즘' 카테고리의 다른 글
| 백준 11051 이항 계수2(dynamic programming) (0) | 2020.07.07 |
|---|---|
| 백준 11722 가장 긴 감소하는 부분수열(dynamic programming) (0) | 2020.07.07 |
| 백준 2294 동전2(dynamic programming) (0) | 2020.07.06 |
| 백준 11048 이동하기(dynamic programming) (0) | 2020.07.05 |
| 백준 6603 로또(bfs) (0) | 2020.07.03 |





댓글 영역